Chapter 1
Introduction to The Method of Lines (MOL)

Extract: …

Elements of the MOL

The basic idea of the MOL is to replace the spatial (boundary value) derivatives in the PDE with algebraic approximations. Once this is done, the spatial derivatives are no longer stated explicitly in terms of the spatial independent variables. Thus, in effect only the initial value variable, typically time in a physical problem, remains. In other words, with only one remaining independent variable, we have a system of ODEs that approximate the original PDE. The challenge, then, is to formulate the approximating system of ODEs. Once this is done, we can apply any integration algorithm for initial value ODEs to compute an approximate numerical solution to the PDE. Thus, one of the salient features of the MOL is the use of existing, and generally well established, numerical methods for ODEs.

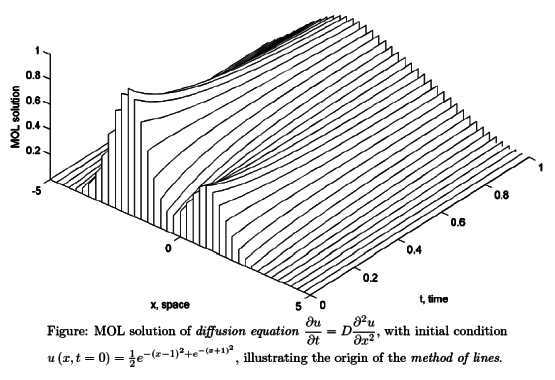
Example Plot: